局部敏感哈希(Locality Sensitive Hashing)
- 前两天写完 Shingling 算法优化,总觉得这么机智的方法其背后一定还隐藏着什么共性的东西。
- 后来想了很久,突然觉得它做的事情好像和局部敏感 Hash相似,查了查资料,果不其然,就是 LSH 里最经典的 MinHash
- 之前一直都是听说过 LSH,但是一直不了解其具体内容,粗略看了一下,发现水还是非常深的。
背景
- 局部敏感哈希和传统Hash不同,传统 Hash 希望即使两个数据有一点点不一样,也要尽可能差异大。而LSH则是希望相似的 value 对应的 Hash 值越相似越好。
- PS:LSH允许小概率的误差
- 常见的使用场景:
- 判重 Near-duplicate detection
- 摘要 Sketching
- 聚类 Clustering
- 相似搜索 Near-neighbor search
定义
- U = Universe of objects
- S: U x U -> [0, 1] = Similarity function
- 对于A,B 的相似性可以用一个hash函数集合$\mathcal{H}$上的概率表示:$Pr_{h\in \mathcal{H} } [h(A) = h(B)] = S(A, B) \ \ (A,B\in U)$
- 由上式可以看出,不同的相似度计算方法,对应着不同的Hash算法
| 相似度度量方法 | LSH算法 |
|---|---|
| Hamming | Sampling Hash |
| Jaccard | Min Hash |
| Angle | Sim Hash |
- Sampling Hash其实就是简单的bit值作为hash
- Min Hash在上一篇文章中已经介绍过了
- Sim Hash是一种基于角相似度的,具体原理介绍请见[1]中的那个ppt,上面有具体的证明
实际中常见的LSH
Min Hash
- 基本和上一篇介绍的一样,这边再简单说下
- 首先切成shingle
- 然后用不同的Hash函数运行多次MinHash过程,然后得到文档签名(signature/sketch)
- 然后根据要求的相似度阀值采割成多个带(band),如果相似,那么肯定有一个band相等

- 按band相等数从大到小两俩计算相似性
SimHash
- SimHash的标准过程和上面讲的MinHash类似,先运行多次,获得签名,然后切割,两两计算相似性
- 不过Google在2007年发布了一篇论文[2],提出了一种估算SimHash签名的算法,效果非常不错,下面简单介绍下这种方法
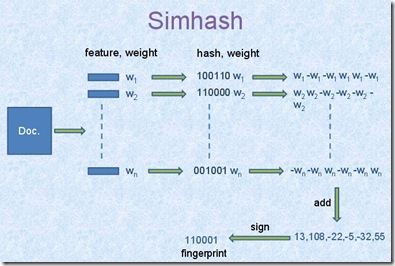
- 如上图,首先获得特征(文本中还是shingle),然后算出每个的hash值
- 然后每位乘以权重,0为-1,求和
- 最后取符号位作为最终的签名
判重
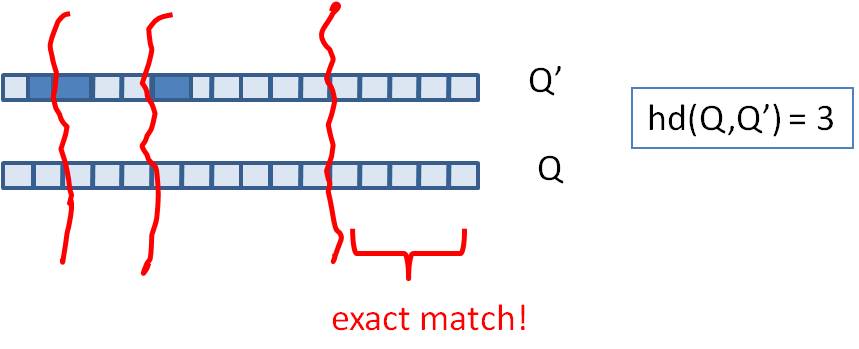
- 上面说的场景都是找Near-neighbor,但还有一类场景是做判重,即返回海明距离小于k的集合
- 在这种情况中中我们不需要两两计算,根据抽屉原理,只需要切割成k+1份band,然后必然有一片是相等的,直接返回集合即可。大大减少了运算量
后记
- 本文只是简单介绍了下LSH,具体的原理,包括什么样的相似性度量方法是LSHable的,推荐看下[1]的ppt
- 这篇文章的写作时间远超想象,本来以为一晚上可以写完,结果写了3天,LSH的理论资料太少了,看了大量在线文章,论文,感觉也只是略知皮毛ಥ_ಥ
留下评论